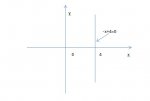
Вопрос Помогите построить прямую (алгебра 7 кл)
- Автор темы Pretender
- Дата начала
Пожалуйста, отключите блокировщик рекламы на нашем форуме.
Я думаю, что нужно решить это уравнение...найти сколько равен х (4) и через эту точку провести прямую...может я ошибаюсь...)
Pretender,Вы наверное очень умны...А задачка то 7 класса... Почему через две точки? По моему и через одну возможно...А значения "у"...паралельно проведите прямую этой оси и любое значение "у" будет Вашим...
Pretender,а через одну точку точно можно построить прямую...
---------- Добавлено в 22:11 ---------- Предыдущее сообщение было написано в 22:09 ----------
тут дело в том что, функциональная зависимость у=f(x) предполагает что при любом значении x функция даёт значение y. В нашем случае х от y не зависит явно, то есть при выполнении выражения x-4= 0 а именно при х=4 у может быть любым от (-inf;inf) то есть вся числовая ось.
---------- Добавлено в 22:12 ---------- Предыдущее сообщение было написано в 22:11 ----------
Pretender, блин, потамучта тут Х постоягная величина, 4, и другой она быть не может...